Извини, но чёрт меня дёргает начать издалека.
ты свистни.. када настроение появиццо))..
Тоту, хорошее начало, издалека, ты продолжай это интересно.
Простые сигналы. Простой сигнал – это одиночный импульс или последовательность импульсов, вида
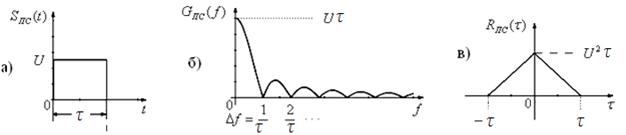
Рис.2.6
Для одиночного импульса мы будем иметь сплошной спектр (рис. 2.6,б), запись которого имеет вид
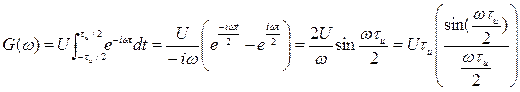
Для последовательности импульсов, или другими словами пачки импульсов - спектр будет иметь дискретный вид.
Размерность спектра (спектральной плотности) импульса будет определяться следующим образом
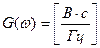
Полоса частот (рис. 2.6,б), где заключено 90% энергии сигнала равна:
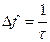
Корреляционная функция простого сигнал (рис. 2,6,в) лежит в пределах от -t¢ до t¢ . Корреляционная функция – это энергия сигнала с размерностью
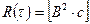
и выражением вида
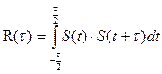
Чем уже корреляционная функция, тем легче, например, в радиолокации осуществить разрешение сигналов и определить параметры до цели по дальности, углу прихода, скорости движения объекта и т.д. Необходимо иметь как можно более острые КФ особенно при близко расположенных целях. Для заострения и укорачивания КФ казалось бы можно брать более короткие сигналы. Однако, энергия сигнала равна
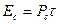
, а это значит, что при уменьшении длительности τ уменьшается энергия сигнала. Следовательно уменьшается дальность обнаружения и соотношение сигнал/шум в точке приема, т.е помехоустойчивость.
База простого сигнала равна
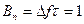Сложные сигналы. Задача сложных сигналов, при той же исходной длительности сигнала τ сформировать узкую КФ, не снижая энергии сигнала. Информационный импульс длительностью τ разбивают на ряд импульсов одинаковой или разной длительностью (рис. 2.7,а).
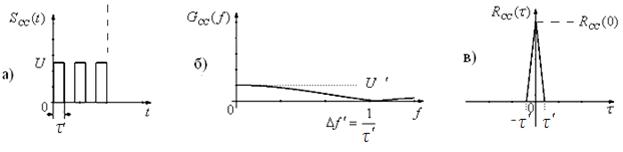
Рис. 2.7
Теперь ширина спектра (рис. 2.7,б) такого сигнала будет определяться самым коротким импульсом t¢, а корреляционная функция (рис. 2.7,в) будет лежать в пределах от -t¢ до t¢ .
Полоса частот, где заключено 90% сигнала равна (рис. 2.7,б):
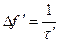
Поскольку энергия по отношению к простому сигналу не изменилась то корреляционная функция (рис. 2.7,в), для сохранения своей площади по отношению к простому сигналу будет лежать выше сложного сигнала.
В свою очередь База сложного сигнала будет равна
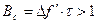
В большинстве случаев большой интерес представляют сигналы с Базой сигнала равной
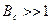
Выражение () определяет собой широкополосный шумоподобный сигнал (ШШС). У такого сигнала структура его приближается к белому шуму, а корреляционная функция стремиться к дельта функции, т.е стремиться в бесконечность.
В качестве
сложных сигналов могут выступать коды Баркера и сигналы линейной частотной модуляции (ЛЧМ).
(
https://lektsii.com/1-170814.html)
