Тем не менее, в Вашем дуализме - если его не утрировать, но Вы этого и не делаете - есть реальный смысл.
На самом деле я это все-таки делаю - утрирую

. Но делаю это специально, чтобы подчеркнуть какие-то моменты, которые мне кажутся важными, но внимания обычно на себе не задерживают. Преднамеренное утрирование с моей стороны порой вызывает чувство протеста, но своей цели оно достигает - эти моменты оказываются в сфере внимания. Причем настолько, что после их можно обсуждать уже в более уравновешенном ключе.
Скажите лучше, Вы знаете людей, которые всерьез занимаются по системе Хинтона?
Вопрос с Хинтоном далеко еще не исчерпан, поскольку с его идеями произошло то же самое - они выпали из внимания большинства его современников, но запали в голову Успенского, что косвенно свидетельствует о недюженности его ума и способности уделять свое внимание вещам, выходящим из сферы обыденности.
Впрочем, и цели у Хинтона и у Успенского были разными, а потому в строгом смысле слова нельзя назвать Успенского последователем Хинтона, т.к. Успенский идеи Хинтона не развивал, а только прикладывал

. По этой части Хинтон похож на ... Карла Маркса, а Успенский на Ленина

. Похож именно тем, что Ленин построил по сути тоталитарное государство, где все средства производства принадлежали не народу (как тому учил Маркс), а элите - партийной верхушке. Тогда как народ по-прежнему работал на этом производстве, как наемные рабочие. Т.е. фактически этот строй был не социализмом, а госкапитализмом. Однако всеми силами натягивал на себя социалистическую личину, утверждая вопреки реальности, что партия - передовой отряд рабочего класса, крестьянства и т.д. Вот и Успенский пытался точно так же натянуть "учение" Хинтона на мистику Гурджиева, тогда как оно на эту мистику не напяливалось

и по сути ничего не давало кроме наукообразных объяснений, которых к практике приложить было нельзя. Тогда как сам Хинтон своей цели достиг, будучи талантливым популяризатором абстрактных математических концепций, причем довольно точно угадавший направление, в котором они будут развиваться в дальнейшем и найдут практическое приложение. Тем не менее, в какой-то мере Хинтон тоже натягивал математику на жизнь, но делал это иначе и с другими целями.
Я не сразу отреагировала на ваше предложение высказаться о "системе Хинтона", т.к. односложный ответ меня не устраивал, а наглядные пособия у меня еще не были готовы

. Поскольку проблема многомерности пространства в своей теоретической основе восходит к математике, то и мои объяснения будут того же типа, т.к. здесь связь с математикой короче всего. Кроме того, понятия, на которые я буду опираться, проходят в
9-ом классе школы, который в пору моего ученичества относился даже не к средней, а к начальной школе

, тогда как для получения среднего образования необходимо было еще закончить 10-ый и 11-ый классы. Поэтому всем, у кого мозги настолько скукожились, что напрочь забыли, чему учились в школе, могут дальше не читать, т.к. каких-то иных средств, типа что-то пососать

или сйожиться в какую-то осану, у меня для них нет. Да и вообще с такими мозгами лучше вообще о многомерных пространствах не задумываться, а ходить с Омом в турпоходы по горам и распевать там у костра песни под балалайку

. Это я не для Evgeny говорю, а для тех, кто сюда забредет по ошибке.
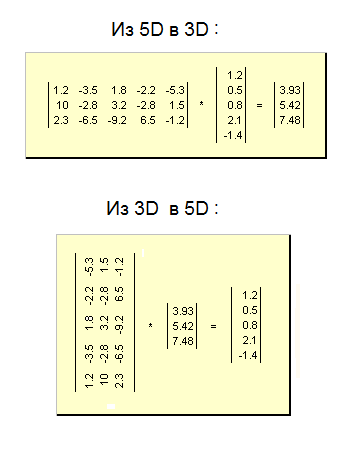
Так вот, в матричной алгебре определено умножение вектора на матрицу, которое дает в результате тоже вектор. Если та матрица квадратная, то и результирующий вектор получится той же размерности, что и множимый. Но если матрица прямоугольная, то размерности исходного и конечного векторов будут разными. На рисунке сверху показан пример превращения 5-мерного вектора в 3-мерный при умножении его на матрицу размером 3x5. По причине эффекта понижения размерности такую операцию часто называют "регрессией". А саму матрицу - "проектором".
Однако возможен и другой вариант, если эту же матрицу повернуть на 90 градусов - рисунок снизу. Теперь на нее можно умножить короткий 3-мерный вектор и получить в результате этого умножения 5-мерный вектор. Оттого-то такую матрицу и назвали "проектором", что она проектирует любые объекты из пространства одной размерности в пространство другой размерности. Однако в случае регрессии (понижения размерности) может порой случиться и так, что несколько разных точек, координаты которых перечислены в 5D-векторе, в результате проектирования попадут на одно и тоже 3D-место. Этот случай вполне ожидаем, поскольку 5-мерное пространство несомненно обладает большей ёмкостью, чем 3-мерное, а потому при сжатии жилплощади нескольких придется класть на одну койку

.
В принципе проектор может быть организован не примитивно в виде умножения на матрицу, как каким-то иным способом. В этом случае его называют уже не матрицей, а оператором. Но суть его работы остается прежней - по-прежнему одно пространство проектируется в другое, хотя только от самого оператора зависит то, как он это делает, т.к. вариантов здесь бесконечно много.
В общем случае совершенно необязательно, чтобы операция проектирования была связана с каким-то деланием и являлась плодом чьих-то трудов. Может случиться и так (и обычно так и случается), что в ходе развития какого-то процесса сфера его действия изменяет свою размерность. И в таких случаях можно говорить о проявлении оператора проектирования, хотя в каком-то самостоятельном материальном виде он не воплощается

. Например, Новый год тоже может прийти не виде деда Мороза, а в виде абстрактного оператора

, проявившего себя в виде смены числа в календаре.
Типичным примером проектирования, сопровождающегося регрессией, является фотография. Здесь 3-мерная натура проектируется в 2-мерное свое изображение. Т.е. проекция получается на единицу меньшей размерности, чем оригинал. Но бывают и обратные случаи. Например, движение планеты вокруг Солнца происходит в одной плоскости. И потому открытие Коперником законов орбитального движения фактически свелось к тому, что он понял, что реальный процесс был более прост, чем то замысловатое движение планет, которое наблюдалось с Земли в телескопы. Вот и сейчас в физиками-теоретиками было обнаружено, что многие процессы (например, в микромире), кажущиеся нам по своему поведению странными и замысловатыми, могут быть истолкованы, как простые до примитивизма процессы в пространстве более высокой размерности, но "искаженные" при проектировании их в нашу 3-мерную реальность. Можно ли на этом основании считать то пространство более высокой размерности существующим реально? Я полагаю, что да

.
Более того, само восприятие нашим сознанием окружающего нас мира тоже подпадает под категорию проекции, т.к. мир в нашем сознании не материальный, а идеальный, а потому и операция проектирования здесь налицо, т.к. пространство реальности и пространство образов различны даже по своей природе, не говоря уже о разнице в размерностях. Собственно противопоставление "Тональ-Нагуаль" непосредственно касается именно этой проблемы.
Разночтение и непонимание здесь возникают исключительно по причине механического понимания размерности, т.к. "придурки"

ничего иного кроме длины, ширины и высоты вообразить себе не могут. Тогда так измерения в механике есть лишь частный случай описания пространства на основе метрических единиц длины. И восходит эта традиция к геометрии, которая когда-то родилась из землемерии, когда важным представлялись лишь размеры садовых участков

. Тогда как алгебра решительно порвала с геометрическими традициями, позволив себе оперировать не только с метрическими длинами, но и вообще с ЛЮБЫМИ количественными параметрами.
Теперь о том, куда все эти измерения деваются

. Здесь надо признать установки Хинтона и Успенского ошибочными. Хотя Хинтону, как популяризатору, это простительно, т.к. обывателям так и положено демонстрировать нечто для них новое исключительно на известных им конкретных вещах. Абстрактного изложения они попросту не поймут. А вот Успенский на полном серьезе искал четвертое изменение в нашем мире, что ему не простительно

.
Суть ошибки Успенского и его учеников в том, что бесполезно искать четвертое или пятое измерение сидючи в собачьей позе с закатанными кверху белками глаз

. Нет там никакого 4-го измерения! И его никак нельзя увидеть и пощупать просто по той причине, что его рядом нет. Тогда куда же оно делось, после того, как произошло "проектирование"? Так вот та ошибка заключается именно в том, что проектирование 5-мерного пространства в 3-мерное ошибочно трактуется так, что два измерения куда-то теряются, типа прячутся от нас, что и вынуждает пускаться на их поиски. Тогда как в действительности здесь происходит сжатие. Типа того, когда в широкую водопроводную трубу врезана узкая труба, через которую вода и хлещет. И здесь глупо задавать вопрос - куда делась остальная вода? Т.к. она никуда не девается, а просто вся сливается через тонкую трубу, какой бы толстой ни была большая труба. Типа как воронка для заливки воды в узкого горлышко. Поэтому высшие измерения не существуют где-то рядом с нами, а попросту ВПРЕССОВАНЫ в наши измерения за счет того самого метода укладывания многих на одну вагонную полку (анекдот есть такой про китайцев, что на поезде ехали, когда их было больше, чем посадочных мест). Вот и тут мы многого не различаем в мире не потому, что оно скрыто в недоступных нашему взгляду измерениях, а лишь по той причине, что очень многое накладывается в нашем восприятии друг на друга, становясь для нас неразличимым.


