Нарисованные человечки могут не считаться с существованием третьего измерения или говорить, что "третье измерение - это время". Могут, потому что на них оттуда не капает.
Нарисованные человечки никогда не скажут такого

Потому что тогда получится, что они уже живут в трехмерном мире. А мы с вами - в четырехмерном!
у нарисованных человеков в их двумерном мире (пространстве) - время так же будет присутствовать, как впрочем и в мире (пространстве) одномерном.
Оно будет присутствовать в любом мире где существует Пространство (имхо).
Evgeny в данном случае прав - действительно корень проблемы именно в том, капают ли на нас из других измерений, и капаем ли мы на них

. А потому озвучу два далеко неочевидных тезиса и постараюсь их защитить.
1.
Пространство - не координатная сетка, а ареал обитания материальных объектов, в котором координатную сетку всегда можно построить. Несложно заметить, что этот тезис исключительно физичен (равно как и материалистичен), но не математичен. Т.е. математики, как поклонники Успенского

, с ним не согласятся. Тем не менее, очень многое в нашем мире указывает на то, что в данном случае к истине ближе физическая трактовка, а не математическая.
В частности, именно физической трактовке лучше отвечает термин "свернутые измерения". Здесь области ареала обитания материальных объектов, которые те перестали посещать, "сворачиваются", а в пределе исчезают совсем. И в обратную сторону - если ареал обитания материальных объектов расширяется, то вполне могут появится новые измерения у занимаемого ими пространства.
В определенном смысле (если сильно не зацикливаться на геометрии) можно сказать, что и субъективный мир человека тоже "свернутый", т.к. за пределами человека этого мира уже нет, оттого-то его часто и называют "внутренним миром" человека. Весьма вероятно, что и в геометрическом смысле пространство нашей Вселенной тоже внутреннее, т.е. за ее пределами известных нам трех измерений уже нет ("свернуты"), да и времени нет тоже

.
С физической точки зрения сперва появляется нечто, что можно измерить, и лишь после этого измерения становятся возможными. Типа того, как размер обуви не мог появиться раньше, чем появились ноги

. Тогда как математики обычно сперва воображают себе координатную сетку, внутри которой представляют появление нового. Поэтому в математике пространство обычного предшествует описанию находящихся в нем объектов. Вот и Успенский более тяготел к математике, чем к физике, потому-то и трактовка пространства у него была именно такая.
2.
Не все существующие измерения равнозначны. Это тезис в какой-то мере вытекает из первого в связи с тем, что одни измерения пространства ареала обитания материальных объектов более густо населены, а другие менее, вплоть до того, когда из-за малой заселенности некоторые измерения сворачиваются. Очень похоже на мертвые города, которые обезлюдели после распада СССР

- их тоже можно с полным правом стереть с географической карты.
А вот причины этого явления более сложны для объяснения. Причем здесь уже математика предлагает эффективные модели этого явления. В частности есть теория линейных операторов, в которой существует понятие о "собственных векторах" (они есть оси координат пространства линейного оператора) и "собственных значениях", которые отражают "мощность" каждого из них. Вот тут тётя интересно про них рассказывает:
 https://ru.coursera.org/lecture/algebra-lineynaya/7-4-sobstviennyie-viektory-i-sobstviennyie-znachieniia-1ji0i
https://ru.coursera.org/lecture/algebra-lineynaya/7-4-sobstviennyie-viektory-i-sobstviennyie-znachieniia-1ji0i Причем, линейный операторы - прямые родственники эвклидова пространства, поскольку они представляют собой класс операций для преобразования линейных размеров объектов, находящихся внутри этого пространства. Т.е. они с понятием пространства по сути едины, поскольку представляют собой свойства этого пространства.
Понятие о "мощности" измерения имеет довольно прозрачную аналогию с габаритами материальных объектов, хотя и характеризует не конкретный объект, а всё пространство, занимаемое данным множеством. Например, такие объекты, как швейная игла или вязальная спица с небольшим допущением можно считать одномерными объектами, поскольку их диаметр мал по сравнению с их длиной. В этом случае можно сказать, что координата собственного пространства вязальной спицы, вдоль которой она ложится во всю свою длину, является более "мощной" координатой, чем две остальные. Или сказать, что эти две маломощные координаты "свернуты" относительно "мощной".
А теперь на наглядном примере посмотрим, что из этих двух тезисов вытекает в практическом плане. Тут уже не так все просто. Хотя для пущей простоты человечков возьмем не двумерных (нарисованных), а одномерных - так оно будет легче разбираться. Теперь смотрим на картинку:
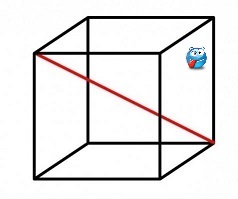
На этой картинке изображен куб, символизирующий 3-мерное пространство, и красная диагональ в нем, символизующая одномерный мир нульмерных человечков (про синюю сбоку морду позже скажу

). Здесь обнаруживаем некоторую терминологическую неувязку, которая присуща и всей этой теме в целом. Дело в том, что несмотря на то, что эта диагональ по меркам 3-мерного пространства одномерна, у каждой из ее точек существуют все 3 координаты. Т.е. точки на диагонали и она сама - полностью равноправные объекты внутри куба, а потому, как и всё внутри него, имеет по 3 измерения. Тем не менее, мы называем эту диагональ одномерной, поскольку она могла бы целиком поместиться в 1-мерное пространство.
Таким образом, мы видим здесь два различных толкования числа измерений, в зависимости от того, имеем ли мы в в виду пространственную "обёртку", в которую можно очертить вокруг нашей Вселенной, или включаем еще что-то, что нашей Вселенной не принадлежит.
Понятие проекции здесь тоже следует применять с осторожностью. Например, ту синюю морду

, которая обитает возле одного из углов куба, можно при желании спроецировать на диагональ, однако она там от этого не появится. Да и вообще не факт, что если эта морда 3-мерна, то она может свободно путешествовать по всему кубу. Очень может быть, что она вообще со своего места сдвинуться не может. Т.е. вопрос свободы перемещения в пространстве напрямую с размерностью перемещающегося объекта не связан. Скажем, молекулы газа можно приблизительно считать нуль-мерными точками, однако это ничуть не мешает им летать по всему нашему 3-мерному космосу.
Здесь возникают интересные вопросы. Не типа дурацкого вопроса "а может ли синяя морда к нам прилететь и перекусить нашу диагональ?"

, а более умный вопрос относительно того, "что мешает 0-мерным человечкам покинуть свою 1-мерную диагональ и путешествовать по всему кубу?". По аналогии с молекулами в космосе, явного запрета на это нет, т.к. 0-мерные точки могут быть быть расположены, как на одной прямой, так и разбросаны в пространстве любой размерности. Причем, синяя морда может быть ограничена в возможностях путешествия по всему кубу ровно по той же причине, что мешает путешествию по нему человечков. Причем этот вопрос для нас принципиальный, т.к. если если таких ограничений нет, но и нет других измерений высшей размерности, и синей морды тогда тоже нет

.
Запрет на путешествия в высших размерностях не может иметь ответ типа "а мы не знали, что туда можно летать"

. Т.е. энтропийные эффекты вынуждают материю распространяться во всех доступных ей направлениях, а потому заповедь "за красную линию не заступать" долго соблюдаться не может - за миллиарды лет кто-нибудь бы такой запрет нарушил, а за ним туда же хлынули и остальные. Типичный тому пример - эффект Комптона, когда свет проходящий через прозрачное вещество способен частично рассеиваться во всех направлениях, вплоть до перпендикулярных направлению светового луча. Причем происходит это не как в бильярде, когда шары соударяются бочком, а когда атом полностью поглощает фотон, а спустя какое-то время испускает его, но у же в случайном направлении. Так вот никакие высшие изменения в той случайности участия не принимают, т.к. иначе бы часть света рассеивалась бы за пределы нашего мира.
Тем не менее, есть и другие объяснения, когда пространственные рамки возможного могут быть уже теоретически допустимого. Взглянем, например, на ... реку и задамся вопросом - почему она течет вдоль своего длинного габарита (длины), а вдоль короткого (ширины) не течет?

А если построить запруду/дамбу, то реку можно превратить в круглое озеро/водохранилище. Примерно так же "мощная" координата способна отсасывать мощность из менее мощных. А наше пространство трехмерно только потому, что запруда его держит, хотя маленько протекает

, вызывая медленный процесс свертки этих трех координат. Ну а время (если его тоже считать координатой) уже свернулось, поскольку на оси времени существует только одна единственная точка - "сейчас".


